Instructions

• This study aims to investigate probabilistic forecasting of effect sizes in psychology.
• You are about to read the description of 9 studies in psychology. All studies feature a comparison between two groups (for example, a treatment and a control group). The studies are recent replications of classic and contemporary findings in psychology conducted as part of a large scale replication project.

Cohen's d Knowledge Test

This study focuses on the effect size measure Cohen’s d for studies in psychology. To assess your prior familiarity with Cohen’s d we will now ask you two questions.

As a rule of thumb - what Cohen’s d values are typically regarded as small, medium, and large in the field of psychology?

Consider a comparison of two groups. The dependent variable in group A has a mean of 3, and that in group B has a mean of 2. The pooled standard deviation equals 2. What is Cohen’s d?

Cohen's 𝞭 Reminder

• Thank you for answering the questions about Cohen's d. Importantly, our study is concerned with Cohen’s 𝞭, the population version of Cohen’s d. This means the focus is on the “true” effect size the way it would manifest itself in a hypothetical study with an infinitely-large sample size.
• Cohen’s 𝞭 expresses the difference between two means in terms of the standard deviation.
• As a rule of thumb: a Cohen's 𝞭 of 0.2 is regarded as small, a Cohen's 𝞭 of 0.5 as medium, and a Cohen's 𝞭 of 0.8 as large.
• The figure below visualizes the overlap of control and treatment condition for different values of Cohen's 𝞭. You can operate the slider to get a feeling for what values correspond to which overlap of control and treatment group.
• Your task will be to specify what effect size you would expect in several studies.

Instructions for Condition 1

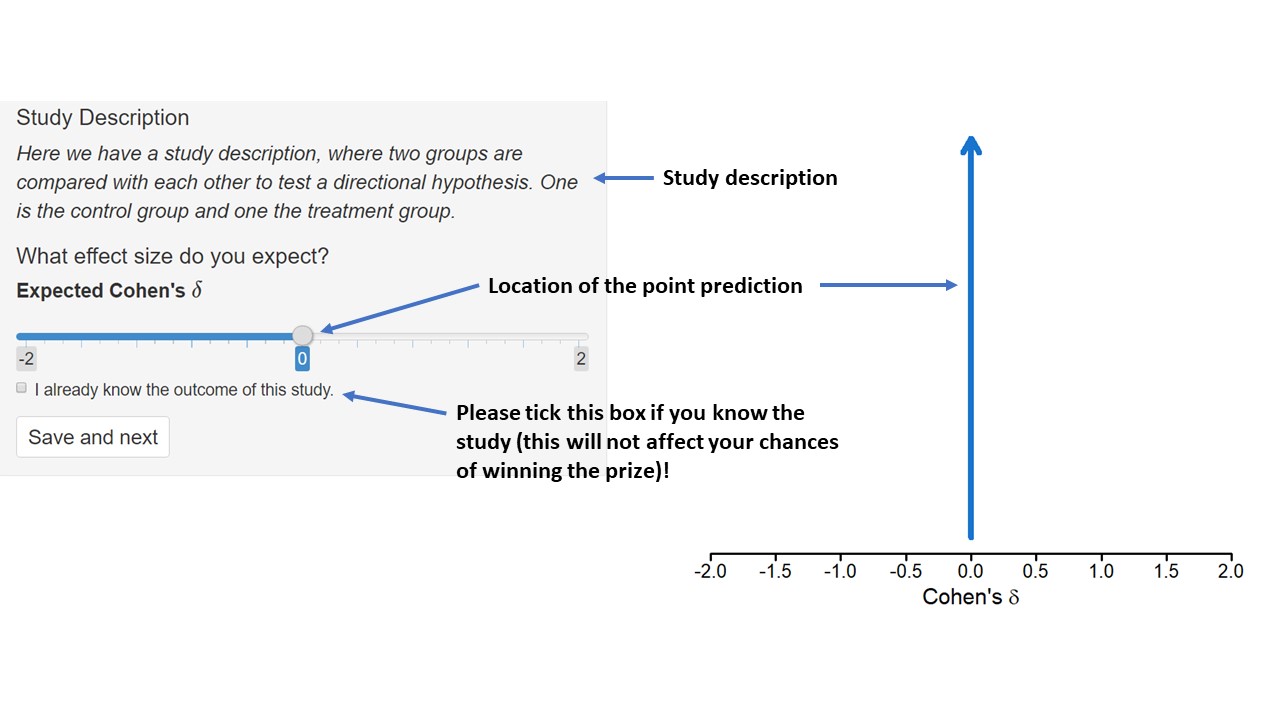
For each study, you will be assigned to one of three conditions where you need to specify the population effect size in different ways. In this experiment you will go through all three conditions. In condition 1 your task will be to specify a point prediction. You can specify your best guess for the effect size with the slider on the left. As you move the slider, the arrow in the graph will move along, representing the value of your best guess. In addition, you can tick the box ''I already know the outcome of this study''. In this case, we will exclude the study for our analysis; however, ticking this box does not affect your probability of winning.

Instructions for Condition 2

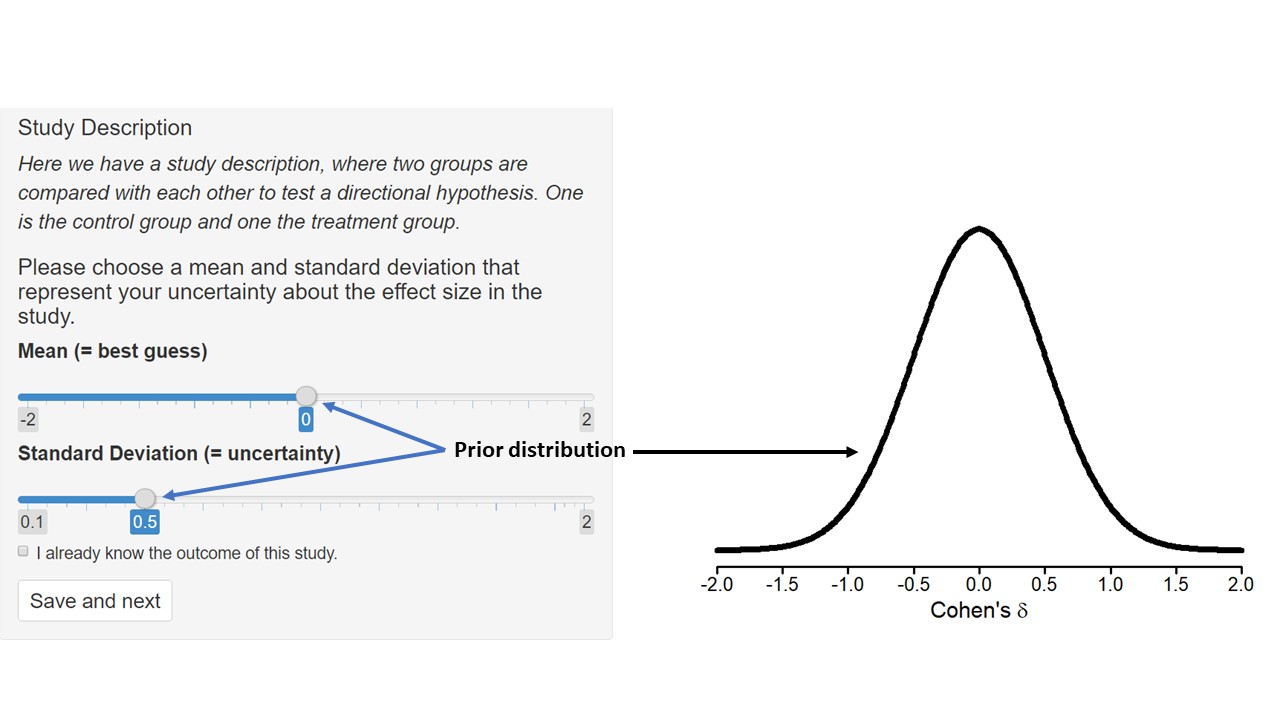
In this condition you specify a prior distribution. A prior distribution represents your uncertainty about the true value of the effect size. To keep things simple, we will use a normal distribution. You can adjust the mean (=best guess) and standard deviation (=uncertainty) of your distribution using the sliders. You should put more mass on values that you consider more plausible and less mass on values that you consider less plausible. The more certain you are the more narrow your distribution should be.

The initial prior distribution that you should adjust is shown below on the right:

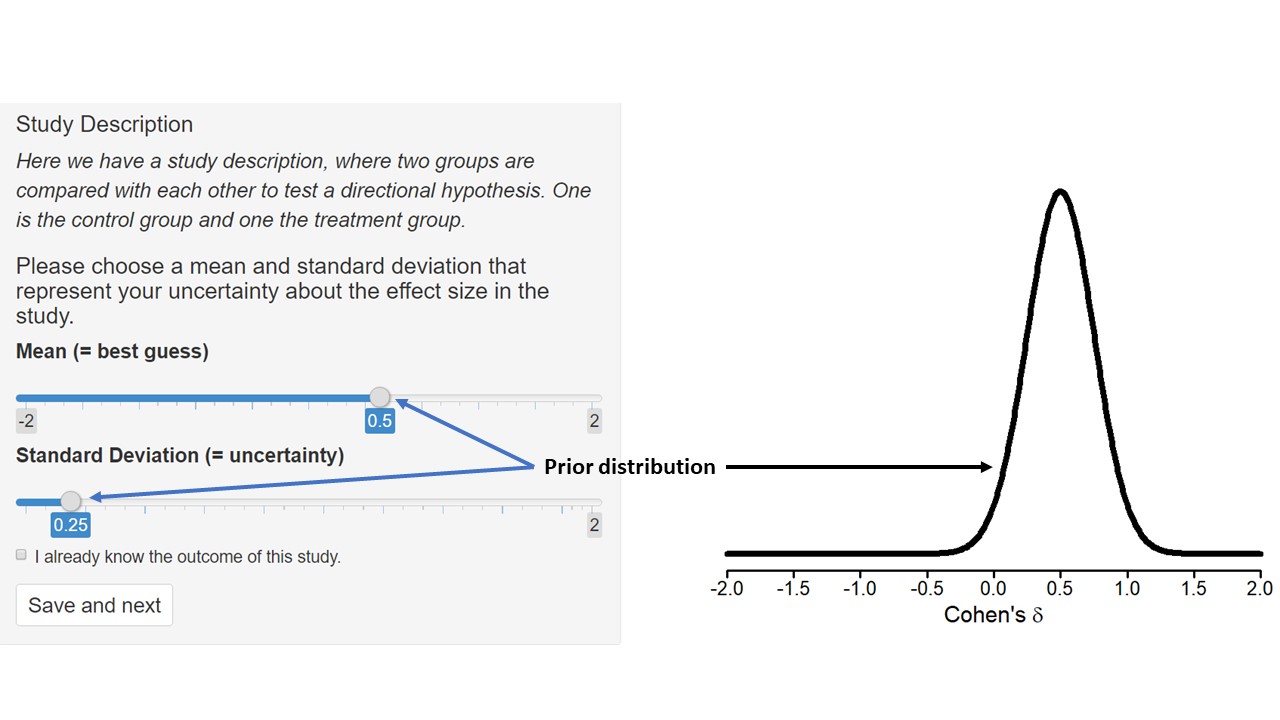
Below is an example that you could specify if your best guess is 0.5 and you are pretty sure that the effect is between 0 and 1.

Instructions for Condition 3

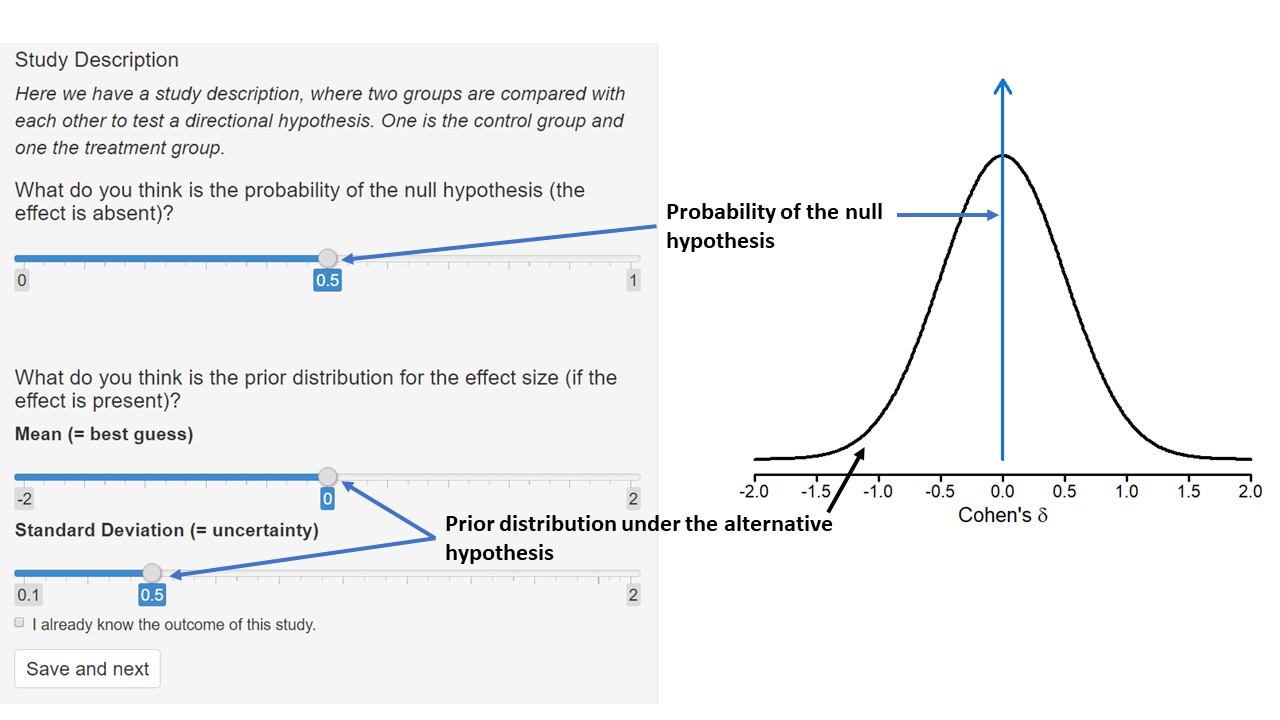
In this condition, you will first be asked to specify the probability of the null hypothesis. If you choose a value of 1, you indicate that you are absolutely certain that the effect does not exist. If you choose 0, this indicates that you are absolutely certain that the effect exists. A value of 0.5 indicates that you believe the effect is as likely to exist as not. Next you will be asked to specify your prior distribution for the effect size under the assumption that it exists.

Please provide more information below as you wish.